Température du moteur :

Je tiens à préciser que tout ce qui suis est avant tout destiné à un usage pratique, et bien qu’il y ait quelques formules pompeuses, je ne suis pas un spécialiste des sciences physiques.

J’ai simplement cherché à comprendre un peu les phénomènes à l’œuvre, sans vouloir dégager de grandes théories.

Le moteur électrique chauffe :

On l’aura tous remarqué, un moteur électrique ça chauffe et ça peut même cramer !

Tout d’abord, il faut comprendre que la température d’un moteur augmente parce que celui-ci produit de la chaleur par effet Joule.

En effet, tout conducteur traversé par un courant va dissiper de l’énergie sous forme de chaleur selon la formule simplifiée :

Q = RI²t

Soit en puissance :

P = RI²

Avec, Q : la quantité de chaleur en Joules,

P : la puissance en Watts,

R : la résistance électrique en Ohms,

I : l’intensité du courant en Ampères,

t : la durée en secondes.

On comprendra alors que : - pour un courant de même intensité, un moteur avec une résistance interne plus faible produira moins de chaleur.

- pour un même moteur, la quantité de chaleur produite sera d’autant plus importante que l’intensité du courant augmente.

A cela il faudrait préciser que la résistance augmente avec la chaleur, ce qui fait qu’un moteur qui chauffe aura tendance à chauffer encore plus !

Le moteur électrique refroidie :

Heureusement, notre moteur ne se contente pas de chauffer indéfiniment. En effet, tout en produisant de la chaleur, il en cède à son environnement immédiat. Pour un moteur bien ventilé, la majeure partie de la chaleur perdue le sera par convection.

En simplifiant à l’extrême, la formule de la transmission de la chaleur par convection peut s’écrire comme suit :

F = hS(T_corps-T_fluide)

Avec, F : le flux énergétique en Watts,

h : coefficient de convection,

S : la surface du corps considéré,

T_corps : la température du corps considéré (°C),

T_fluide : la température du fluide (°C).

On comprendra alors que plus le moteur est chaud par rapport à l’air ambiant, plus il perdra de la chaleur. Ainsi la température du moteur se stabilisera lorsqu’il perdra autant de chaleur qu’il en produira.

La valeur de h dépend d’une multitude de facteurs que je me garderais bien d’aborder ici. D’une façon pratique j’utiliserais le produit hS sous le terme de coefficient de convection. Coefficient qui nous permettra de caractériser différents moteurs sous certaines conditions.

Quel lien entre chaleur et température ?

La chaleur ce n’est pas la température, mais la température d’un corps augmente selon la quantité de chaleur absorbée.

On parlera de la capacité thermique massique d’un corps pour connaître la quantité de chaleur nécessaire à l’augmentation de sa température :

dT = C.dQ

Avec : dT : la différence de température,

C : la capacité thermique massique,

dQ : quantité de chaleur.

Ainsi, la variation de la température est plus ou moins proportionnelle à la quantité de chaleur apportée.

Au final, comment chauffe un moteur électrique ?

Un moteur électrique en marche va donc se mettre à produire une certaine quantité de chaleur par unité de temps. On parlera d’un flux de chaleur ou puissance.

Sous l’effet de cette chaleur produite, sa température va augmenter rapidement dans un premier temps. Or plus sa température augmente par rapport à celle de l’air ambiant plus le flux de chaleur dissipée par convection va augmenter. La somme totale des deux flux de chaleur va alors diminuer jusqu’à atteindre un équilibre : le moteur produit autant de chaleur qu’il n’en perd par convection, sa température ne varie plus.

Pour vérifier tout ça il nous faut comparer des données mesurées à celle que l’on aura calculées.

Pour connaître la température du moteur en fonction du temps, je traduirai alors l’expression par la formule suivante :

T_moteur(t=n) = T_moteur(t=n-1) + Cm.( Ri.U² - Cc.( T_moteur(t=n-1) – T_air))

Qui permet de calculer seconde après seconde la température théorique du moteur, connaissant sa température de départ, la température de l’air ambiant, sa résistance interne (Ri) et en jouant avec deux coefficients.

Cm, le coefficient « massique » et Cc, le coefficient « de convection ».

Pour peaufiner, on se basera sur une modification de la résistance interne avec la température.

D’un autre côté, on a fait une série de mesures sur différents moteurs à différents courants. La température du moteur est prise par un capteur qui renvoi la température toute les 30 secondes environ (démonté sur un capteur de station météo bon marché).

La température mesurée est certes approximative mais cela n’a pas beaucoup d’importance.

Le moteur est donc envoyer plein gaz pendant un certain temps. L’intensité baisse au fur et à mesure que le moteur chauffe et que la résistance augmente.

La température est notée toutes les 30 secondes en veillant à ne pas dépasser 60 à 70°C.

On peut ensuite graphiquement en déduire les deux coefficients de sorte que la courbe « théorique » coïncide avec les valeurs mesurées.

fig.1 : N2826-1350, poids = 51g , Cm = 0,0370 , Cc = 0,515.

fig.2 : N2830-1000, poids = 62g , Cm = 0,0300 , Cc = 0,420.

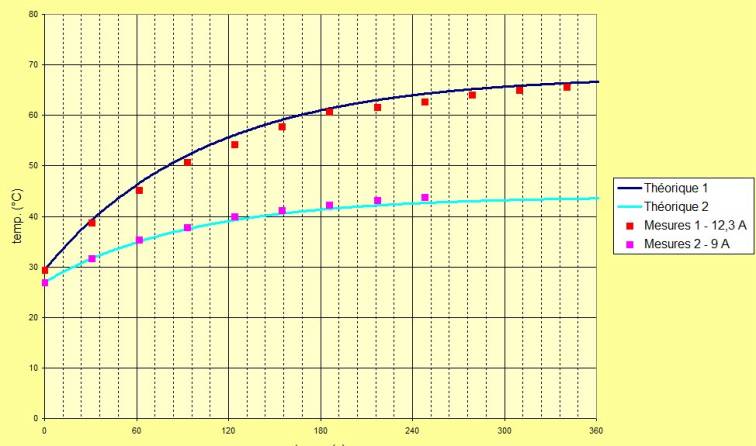
fig.3 : N2836-880, poids = 76g , Cm = 0,0245 , Cc = 0,460.

Bien que la méthode soit un peu barbare et source de multiples approximations la corrélation est évidente.

Bien logiquement, le coefficient « massique » est inversement proportionnel au poids du moteur. Les valeurs du coefficient « de convection » soit moins évidente à interpréter, elles dépendent certainement de la surface soufflée et de la vitesse de l’air brassé par l’hélice. Dans l’ensemble, le coefficient « de convection » estimé varie entre 0,4 et 0,6 sans que l’on puisse faire de corrélation évidentes avec un facteur précis.

Et ça sert à quoi tout ça ?

On peut s’intéresser à la température atteinte en fonction de l’intensité du courant et ainsi avoir une idée de la puissance maximale d’un moteur.

On sait que cette température va dépendre de divers facteurs : le poids du moteur, sa résistance interne et la qualité du refroidissement.

Pour la suite on considèrera le coefficient de « convection » comme étant constant, ce qui n’est bien évidemment jamais le cas mais nous permettra de nous concentrer sur les autres facteurs, qui sont naturellement plus constants.

On peut faire un lien quasi direct entre le poids et le KV d’un moteur et sa résistance interne.

En effet, d’un point de vu purement pratique on peut poser comme hypothèse que pour deux moteurs identiques la résistance des bobines variera avec le carré du nombre de spires. Or le nombre de spires étant inversement proportionnel au KV il s’en suit que la résistance interne variera avec l’inverse du carré du KV, autrement dit :

Ri = a / KV²

Où a est une constante pour des moteurs de même poids et de même construction.

fig.4 : résistance interne de 3 brushless de même poids mais de KV différents, selon 1/KV².

Or, on peut établir une relation entre la constante a = Ri.KV² et le poids du moteur. Pour des moteurs similaires, Ri.KV² varie avec l’inverse du carré du poids :

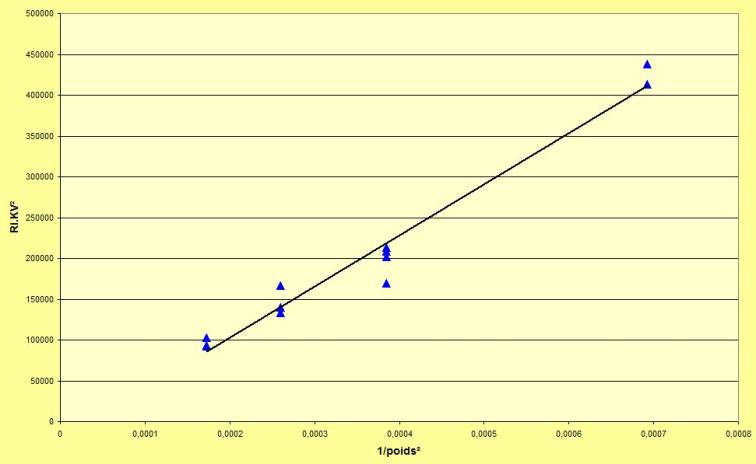
fig.5 : Ri.KV² selon l’inverse du poids au carré, pour des moteurs similaires.

Au final, on pourra établir une relation entre Ri, le poids et le KV du moteur, comme suit :

Ri = k / ( KV².poids²)

Cela semble valable pour des moteurs de la même gamme.

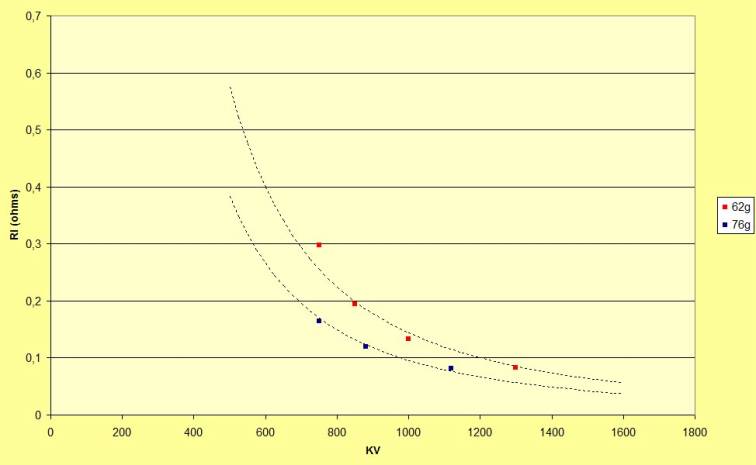
fig.6 : Résistance interne selon le KV de moteurs de 62g et 76g.

Evidemment, il existe une bonne marge d’erreur, les petits moteurs ayant tendance à avoir une résistance plus élevée que pour le modèle idéal. Et j’ai probablement bafoué deux ou trois lois fondamentales de la physique mais…

Néanmoins, on va pouvoir faire quelques comparaisons (en restant dans le domaine théorique).

Premièrement, le graphe ci-dessous nous montre que pour des moteurs de même KV l’intensité du courant nécessaire pour atteindre une certaine température d’équilibre est proportionnelle au poids du moteur.

Autrement dit, la puissance maximale admissible en continue est proportionnelle au poids du moteur !

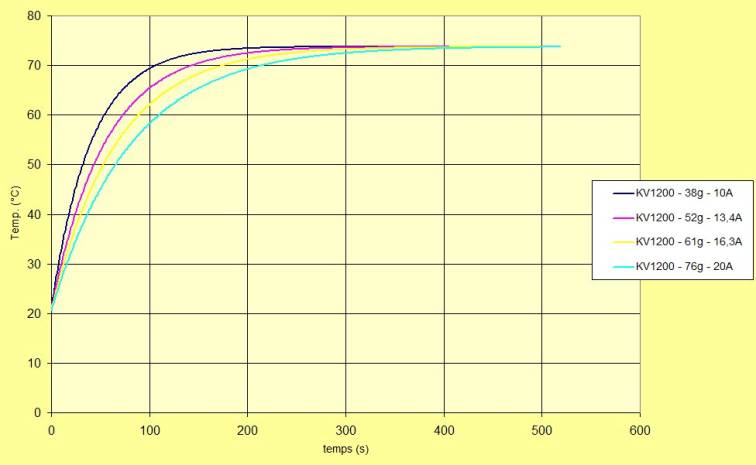
fig.7 : montée en température de 4 moteurs de même KV.

Deuxièmement, on notera que l’influence du KV est similaire à celle du poids :

fig.8 : intensité nécessaire pour atteindre la température d’équilibre selon le KV.

Magnifique graphe…